Introduction
Secure communication is critical, for e-commerce, e-banking, and even e-mail. Additionally, systems are becoming even more distributed (pervasive computing, grid computing, as well as other systems - on-line gambing or MMOGs). We know that the real world has many people who will try to gain advantage. Mischief in the virtual world is typically remote and faceless.
In the real world, we want confidentiality, secrecy and privacy - criminal offences exist to prosecute unauthorised opening of mail. Integrity is also an important aspect, it should be apparent when artefacts have been altered - seals have been used in years gone by to protect documents. Similarly, the authenticity of artefacts needs to be proved.
Other things we want in the real world includes non-repudiation (you should not be able to deny doing specific actions, for example if you bought a share you should not later deny it), which is often implemented using the idea of signatures and witnessing (but reputation is still important in this system). Similarly, recorded delivery aims to protect against denial of the receipt of goods.
We also want to have anonymity if need be, and also validation of properties (usually by some expert, e.g., certificates of authenticity).
Variants of all these properties, and more, exist in the digital world - there are plenty of opportunities for mischief. Tools ared needed to enable these sort of properties to be guaranteed in digital systems - cryptography lays at the heart of providing such tools and guarantees in digital systems.
Cryptography by itself is not security, but it can make a very significant contribution towards it.
Loosely speaking, we are interested in two things, making intelligible information unintelligible (i.e., scrambling it in some way), and also making unintelligible information intelligible. These processes are generally known as encryption and decryption.
Cryptographers are the people who supply us with mechanisms for encrypting and decrypting data, and they are in a perpetual war with the cryptanalysts - the code breakers. Often these people work on the same side and together in order to improve security.
Data in its normal intelligible form is called plaintext. This data is encrypted into
messages unintelligible to the enemy, and these are called ciphertext. In modern computer-based cryptography, the plaintext and ciphertext alphabets are simply {0,1}, but traditionally were the alphabet.
A typical block diagram of the process looks similar to this:
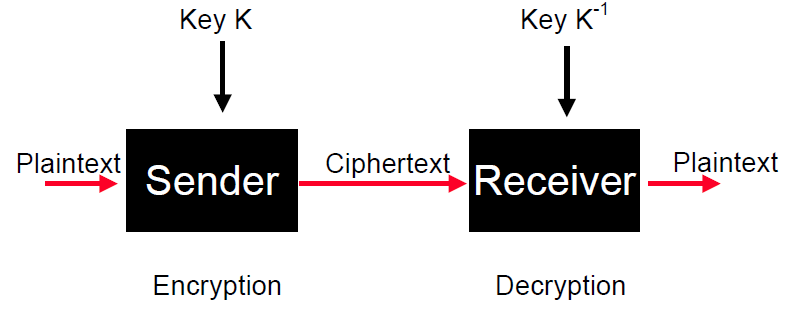
Additionally, we also need a secure channel to ensure the appropriate keys are possessed by the sender and receiver.
Private and Public Cryptography
Two major approaches to cryptography are the private, or symmetric, key cryptography approach and the public key approach. In the private key, the encrypting and decrypting keys K and K-1 are the same (are one is easily derivable from the other). With public key cryptography, the two keys are different, and it is very difficult (without special knowledge) to derive one key from the other.
Public key cryptography has arisen in the last 30 years, and has been invented more than once: first secretly by GCHQ's Cox and Ellis, and then publicly by Diffie and Hellman. Private key cryptography has a much longer history.
Attacks
With massive computational power become available, such as grid computing, or using cheap specialised hardware such as FPGAs, brute force attacks are possible.
Another general idea of cryptanalysis is to detect and exploit structure in the relationship between plaintext inputs, the key used and the ciphertext outputs. This can be used to derive keys, but weaker breaks are important - being able to tell what type of cryptographic system a stream is encrypted with gives us a foot in the door, as you should not be able to tell random streams apart. This attack detects leaking strcture.
The general idea of cryptographic systems it to make the plaintext to ciphertext mapping as random looking as we can. Sometimes, using an attack by approximation, we can detect a structural relationship in the operation of an algorithm, which exists with some small bias (i.e., an apparent deviation from random-ness).
Some schemes are based on the assumed computational difficulty of solving instances of particular combinatorial problems (e.g., knapsacks, perceptron problems, syndrome decoding). Solving such problems may not be as hard as we think. As NP-complete is about the worst case, cryptography cares more about the average case.
Cryptography is based on the idea that factorisation really is hard.
We can also attack the implementation. Mathematical functions simply map inputs to outputs and exist in some conceptual space, but when we have to implement a function, the computation consumes resources: time and power.
Encrypting data with different keys may take different times. The key and the data affects the time taken to encrypt or decrypt, which gives a leakage of information about the key. Even monitoring power consumption may reveal which instructions are being executed.
Classical Ciphers
All classical ciphers work by doing plaintext substitution (replacing each character with another), or transposition (shuffling the characters). These are very easy to break and no longer used, but are instructive since some cryptanalytic themes recur in modern day cryptanalysis.
Caesar Ciphers
The Caesar cipher works by shifting letters of the alphabet some uniform amount, e.g., if it was a Caesar cipher of 3, A becomes X, B becomes Y, etc, so BAD becomes YXA. This is hardly the most difficult cipher to break. These classical ciphers operate on characters or blocks of characters (modern implementations operate on bits, or blocks of bits).
This early cipher was used by Julius Caesar, and works on the normal ordered alphabet, and shifts letters by some number - this number is the key k. If we map the alphabet onto the range of integers 0-25, then the Caeser cipher encrypts the characters corresponding to x as the character corresponding to (x + k) mod 26.
As there are only 26 keys, it is simple to brute force this cipher. Occasionally, we may get more than one possible decryption, but this is only likely if there is a very small amount of ciphertext.
Substitution Ciphers
A simple substitution cipher is simply an injective mapping: f : Π → Π, where Π is the alphabet.
All instances of a word are enciphered in exactly the same way. The appearance of these repeated subsequences in the ciphertext may allow the cryptanalyst to guess the plaintext mapping for that subsequence (using the context of the message to help).
If you actually know some of the plaintext, than these sort of ciphers are fairly trivial to break, you don't need much in the way of inspired guessing.
This problem arises because identical plaintexts are encrypted to identical ciphertexts.
Another possible attack arises due to the nature of natural language - in particular, the frequency of character occurence in text is not uniform. Some characters are more common than others, e.g., "e" in English text, as well as pairs (bigraphs), "th", etc.
Unfortunately for simple substitution ciphers, this structure in the plaintext is simply transformed to corresponding structures in the ciphertext. If the most common ciphertext character is "r", then there is a good change that it will be the encryption of "e" (or one of the other highly frequent characters).
One thing to be aware of is that the frequency tables are compiled using a great deal of text, any particular (especially true if the ciphertext is shorter) text will have frequencies that differ from the reference corpus. Thus, mapping the most frequent ciphertext character to the letter "e" may not be the right thing to do, but mapping it to one of the most popular characters probably is.
One way to address this problem is to allow each character to be encrypted in multiple ways, or use multiple ciphers.
One solution homophonic substitution, that is. to have a separate (larger) ciphertext alphabet and allow each plaintext character to map to a number of ciphertext characters. The number of ciphertext characters corresponding to a plaintext character is directly proportional to the frequency of occurrence of the plaintext character.
e.g., I has a frequency of 7 compared to V's 1, so I would map to 7 characters and V would map to 1. In this way, the ciphertext unigram statistics become even.
Vigenere made an extremely important advance in classical ciphers. He chose to use different ciphers to encrypt consecutive characters. A plaintext is put under a repeated keyword, with the character for that particular point to index the actual cipher used.
This appears to solve the problem - the statistics are flattended, but if we were to measure the frequencies of subsequences of the ciphertext (e.g., for key length 4: subsequences, 1, 5, 9, 13, etc, and 2, 6, 10, 14, etc...), we might expect these frequencies to be approximately those of the natural language text as usual.
In order to figure out the size of the keyword, or the period of the cipher, we look for n-grams occurring frequently in the ciphertext (e.g., frequent bigrams, trigrams - the bigger the better). The chances are that they correspond to idential plaintext enciphered with the same component ciphers (positions at some multiple of the period).
Once we have this period, we can apply earlier frequency analysis to each component cipher. Bi-graph frequencies can help too.
Substitution ciphers have a nice property - keys that are nearly correct give rise to plaintexts that are nearly correct. This allows from some interesting searches to be carried out. If you can measure how "good" your current key guess is, you can seek over the keyspace in order to maximuse this measure of goodness.
Of course, we can not know how good our current key guess is without knowing the actual plaintext, but we can use frequency statistics under decryption to key K to give us a strong hint.
A typical search starts with a key K (a substitution mapping), which makes repeated moves swapping the mapping of two characters, with the general aim of minimising the cost function derived from the frequency analysis. This is non-linear, and you run the risk of getting stuck in local optima.
Transposition Ciphers
Transposition ciphers "shuffle" the text in some way - a simple transposition cipher f might permute consecutive blocks of characters, e.g., for a reversal permutation: f = (4, 3, 2, 1), encryptf(JOHNHITSJOHN) = NHOJSTIHNHOJ.
To create a transposition cipher, we chose a period L, and a permutation of the numbers 1..L. The plaintext is then written out in rows of length L, and the columns are labelled according to the permutation chosen (e.g., 6 3 1 2 5 4), and then the columns reorganised in ascending order according to their label.
Unigram statistics can be used to tell us this is a transposition cipher, as the statistics will be very similar to that of plaintext.
Bi-gram statistics are rather important, and we can use similar sort of tricks as earlier to determine the period. If you guess the period wrongly, and try to find a permutation, you will be hard pressed to find pairs of columns in the decryption which have appropriate bigram statistics when considered consecutively. If you guess the period correctly, then it is possible to find pairs of columns with good bi-gram frequency statistics.
We can do searches over the permutation to find the approximate order (using the bigram cost function identified earlier).
We can also use the dictionary (or a subset of it, most people only use a limited amount of it in daily conversation) to scan the obtained plaintext to see whether it contains known words. If it does, this suggests that corresponding parts of the key are correct - this has been greatly facilitated by computers.
This theme of power being obtains due to guessing correctly, and then being able to do so again in the future is important and will return again.
Stream Ciphers
A common simple stream cipher works by generating a random bit stream, and then XORing that stream on a bit by bit basis with the plaintext. This is called a Vernan cipher.
This depends on both the sender and receiver having synchronised streams of both ciphertext, and the keys - packet loss would send the streams out of synch. A very large amount of work has been done on random stream generation, it's more difficult than it first appears.
Linear Feedback Shift Registers
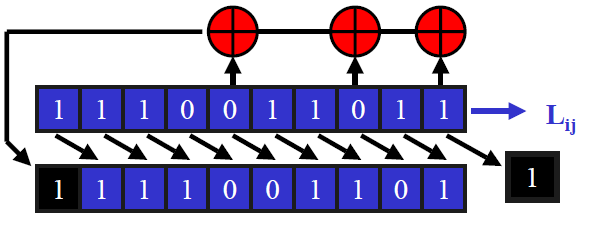
At each iteration, there is a right shift, a bit fall off the end and the leftmost bit is set according to the linear feedback function.
We want the stream to be random looking. One feature should be that the stream should not repeat itself too quickly. As this is, in effect, a finite state machine, it will repeat itself eventually, and the maximal period for an n-bit register is 2n-1 (it can not be 2n as if the register was all 0, it would get stuck).
The tap sequence defines the linear feedback function, and is often regarded as a finite field polynomial. You have to choose the tap sequence very carefully. Some choices provide a maximal length period, and these are primitive polynomials.
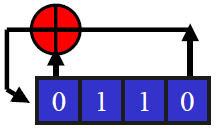
The above polynomial has a maximum period, and it is common to denote this as C(D) = 1 + D + D4. A similar polynomial, C(D) = 1 + D + D3 does not give a maximal period sequence.
This kind of implementation is not good for pseudo-random number generation. If we had a 64-bit register, then once we know a very small amount of plaintext (e.g., 32 consecutive bits), then you can calculate the corresponding key stream and so know the rightmost 32 bits of the register. The remaining 232 bits can be brute forced quite easily, and when you get the right one, the whole key stream should be generated.
This is far too easy to break, but LFSRs are very easy to implement, and are fast. To fix matters, we can use a less primitive way of extracting the key stream, or even combining several streams to achieve better security.
A very simple model would involve using some function, f to operate on some subset of the LFSR register components.
Algebraic Normal Form
A boolean function on n-inputs can be represented in the minimal sum (XOR, or +) of products (AND .) form:
f(x1, ..., xn) = a0 + a1.x1 + ... + an.xn + a1,2.x1.x2 + ... + an - 1, n.xn - 1.xn + ... + a1, 2, ..., n.x1.x2...xn.
This is called the algebraic normal form of the function.
The algebraic degree of the function is the size of the largest subset of inputs (i.e., the number of xj in it) associated with a non-zero co-efficient.
e.g., 1 is a constant function (as is 0). x1 + x3 + x5 is a linear function, x1.x3 + x5 is a quadratic function, etc.
A very simple model with a linear f would be pretty awful. If we knew a sequence of keystream bits, then essentially every key stream output can be expressed of a linear function of elements of the initial state. We can derice a number of these equations and then solve them by standard linear algebra techniques.
A non-linear f is slightly better, but it is still possible to attack such systems if f is approximated by a linear function.
Please see slide 5
for more detail.
Given f(x1, ..., xn), it is fairly straightforward to derive the ANF. If we consider the general form, the constant term a0 is it is f(0, ..., 0) (the 0's cancel out any other term).
Classic Model
The classical model involves a series of n-bit registers with some function f, where the initial register values form the key.
The LFSRs need not all be the same length, and the LFSRs will give a vector input which has a period that is the product of the least common multiple of the periods of each of the LFSRs.
An awful choice for f would be f(x1j, x2j) = x1j. If the LFSRs were 32-bits long, this would disregard 32 of those bits, leading to our key size to be effectively 32 bits.
XOR would use all 64 bits, but would still not be a good choice. If the stream bit is 0, then there are only 2 possible pairs - similarly if the stream value is 1. This again reduces our key size to 32 bits.
These examples are extreme, but beware of linearity, even a hint of it can cause weaknesses.
Divide and Conquer Attacks
A Geffe generator works by using a nx1 multiplexor, with n + 1 LFSRs, with one being used for select. For a 2x1 multiplexor, this gives us the equation: Z = (a & b) + (not(a) & c).
If we put this into a truth table, we see that the output Z agrees with b 75% of the time, and also agrees with c 75% of the time.
If we consider each possible initial state s of the second register and then determine the stream produced from this initial state, we can check the degree of agreement of this stream with the actual key stream. If state s is correct, we will get roughly the right amount of agreement. If it is incorrect, the agreement will be roughly random.
We can target the third register in exactly the same way, and then can derive the first register (the selector) very easily by trying every possible state. The correct one would allow us to simulate the whole sequence. There are other ways too.
These divide and conquer attacks were suggested by Siegenthaler as a means of exploiting approximate linear relationships between function inputs and its ouput. This led to new criteria being developed as countermeasures to these correlation attacks.
If we have two functions f(x1, x2) and g(x1, x2), we say that f(x1, x2) is approximated by g(x1, x2) if the percentage of pairs (x1, x2) which given the same values for f and g differs from 50%.
If they agree precisely half the time, we say that they are uncorrelated. If the agreement is less than 50%, we can do g(x1, x2) + true to find a function with positive agreement.
We can consider similar ideas for n-input functions: f(x1, x2, ..., xn) and f(x1, x2, ..., xn). The degree of approximation with linear functions may be slight, and the smaller the degree of approximation, the more data you need to have to break the system.
The idea of multiple LFSRs is that the size of the keyspace should be the product of the keyspace sizes for each register. Divide and conquer reduces this to a sum of key sizes, and you can attack each in turn. When you crack one LFSR, the complexity of the remaining task is reduced (e.g., f(x1, x2) = x1.x2 + x1 - once you know what x1 is, then whenever you know x1 = 1, you know what x2 is).
In a similar vein, if we suppose there is a small exploitable correlation with input x1 and there is a small correlation with x1 + x2. If LFSR can be broken to reveal x1, then we now have a straightforward correlation with x2 with which to exploit.
All these attacks assume you know the tap sequence. If you kept the feedback polynomial secret (i.e., make it part of the key), this makes things harder, but there are in fact some further attacks here too.
Boolean Functions
Boolean functions are, unsurprisingly, those of the type: f : {0,1}n → {0,1}. We can also consider a polar representation (f^(x)), where f^(x) = (-1)f(x).
Boolean functions can be regarded as vectors in R2n with elements 1 or -1 (derived from our polar form). Any vector space has a basis set of vectors, and given any vector v, it can always be expressed uniquely as a weighted sum of the vectors in the basis set.
If the basis vectors are orthogonal and each have a normal length (1), we can say they form an orthonormal basis. We can express any vector in terms of its projections onto each of the basis vectors.
Given a basis, you can always turn it into an orthonormal basis using the Gram-Schmidt procedure. Given an orthogonal basis, you can always create an orthonormal one by dividing each vector by its norm.
n-dimensional vectors can be normalised in the same way, the norm is the square root of the sum of the squres of its elements.
Linear Functions
If we recall that for any ω in 0..(2n - 1), we can define a linear function for all x in 0..(2n - 1) by Lω(x) = ω1x1 XOR ... XOR ωnxn, where ω and x are simply sequences of bits.
We will use natural decimal indexing where convenient (e.g., ω = 129 = 10000001).
The polar form of a linear function is a vector of 1 and -1 elements defined by L^ω(x) = (-1)omega;1x1 XOR ... XOR ωnxn = ∏nj = 1(-1)ωjxj.
One criterion that we may desire for combining function is balance (that is, there are an equal number of 0s and 1s in the truth table form, and there are an equal number of 1s and -1s in the polar form), so the polar form has elements that sum to 0, or, if you take the dot product of the polar form of a function with the constant function comprising all 1s, the result is 0.
Each linear function has an equal number of 1s and -1s (and so is a balanced function).
Dissimilar linear functions are orthogonal. If we consider the dot product of any two columns of the 8×8 matrix given in the slides, the result is 0.
The linear functions are vectors of 2n elements each of which is 1 or -1, the norm is therefore 2n / 2, and thus we can form an orthonormal base set.
Since a function f is just a vector, and we have an orthonormal basis, we can represent it as the sum of projections onto the elements of that basis using the Walsh Hadamard function.
Various desirable properties of functions are expressed in terms of the Walsh Hadamard function, e.g., balance means that the projection onto the constant function should be 0.
We saw that functions that looked like linear functions too much were a problem, but a measure of agreement is fairly easily calculable (Hamming distance with linear function in usual bit form, in polar form, we simply take the dot product of the linear function).
A function f that has minimal useful agreement (i.e., 50% agreement) with Lω has Hamming distance 2n / 2 with it (or, in polar terms, half the elements agree and half disagree). If all the elements disagree (i.e., f = not Lω), we can form another function that agrees with Lω entirely by negating f (i.e., f + 1).
If correlation with linear functions is a bad idea, let's have all such correlations equal to 0 (i.e., choose f such that the projections onto all linear functions are 0). This is not possible, however. Because we have a basis of linear functions, if a vector has a null projection onto all of them, it is the zero-vector.
A Boolean function is not a zero-vector, it must have projections onto some of the linear function. But some projections are more harmful than others, from the point of view of the correlation attacks.
These correlations with single inputs are particularly dangerous, with the danger decreasing proportional to the number of inputs.
Correlations with single inputs correspond to projections onto the Lω where the ω has only a single bit set. Similarly, correlations with linear functions on two inputs correspond to the projections onto the linear functions Lω where the ω has only two bits set.
If a function has a null projection onto all linear Lω functions with 1, 2, ..., k bits set in ω (i.e., it is uncorrelated with any subset of k or fewer inputs), the function is said to be correlation immune of order k. If it is also balanced, then we say it is resilient.
For a variety of reasons (there are other attacks that exploit linearity), we would like to keep the degree of agreement with any linear function as low as possible. If we can not have all that we want (all projections 0), we can try to keep the worst agreement to a minimum.
This leads to the definition of the non-linearity of a function. We want to keep the Hamming distance to any linear function (or its negation) as close to 2n / 2 as possible. Or, keep the maximum absolute value of any projection on a linear function to a minimum, that is, keep maxω|F^(ω)| as low as possible.
Non-linearity is defined by: Nf = 0.5(2n - maxω|F^(ω)|). It seems to minimise the worst absolute value of the projection onto any linear function, but what is the maximum value we can get for non-linearity?
We can project these vectors onto a basis of 2n orthogonal (Boolean function) vectors L0, ..., L2n - 1, where Lω(x) = ω1x1 XOR ... XOR ωnxx.
Bent functions were first researched by Rothuas, and maximise non-linearity, and are function based on even number of variables. Bent functions have projection magnitudes of the same size, but with different signs. This includes projection onto the constant function, not a balanced function, therefore if you want maximum non-linearity, you cannot have balance.
Additionally, non-linearity and correlation immunity are in conflict, as it requires an increase in the magnitude of the vectors.
All other things being equal, we would prefer more complex functions to simpler ones. One aspect that is of interest is the algebraic degree of the function, which we would like to be as high as possible.
This causes a conflict with correlation immunity. Sigenthaler has shown that for a function f on n variables with correlation immunity of order m and algebraic degree d, we must have m + d ≤ n, and for balanced functions, we must have m + d ≤ n - 1.
There is another structure that can be exploited. It is a form of correlation between outputs corresponding to inputs that are related in a straightforward way. This is autocorrelation.
We begin to see the sorts of problems cryotpgraphers face. There are many different forms of attack, and protecting against one may allow another form of attack. However, given the mathematical constraints, we might still want to achieve the best profile of properties we can - a lot of Boolean function research seeks constructions to derive such functions.
There is no such thing as a secure Boolean function. There may be functions that are appropriate to be used in particular contexts to give a secure system, however, the treatment here shows quite effectively that life is not easy and compromises have to be made.
Block Ciphers
Another modern type of cipher is the block cipher, which is very common. They work by taking a block of data (e.g., 64, 80, 128 bits, etc) and transform it into a scrambled form (itself a block of the same size).
The encryption key K determins the mapping between the plaintext blocks and the ciphertext blocks. Without a knowledge of the key, this should look like a random association.
In the examples on the slide, this key is expressed by citing the whole permutation, however in practice this would be very difficult. Usually, a key consists of a number of bits, the value of which together with the algorithm defines a functional relationship between the input and output blocks.
Defining this relationship by enumeration is rare, except for very small components of an algorithm.
There are many different block ciphers, the most common are DES (Data Encryption Standard), LUCIFER (a precursor to DES), IDEA (used in PGP) and AES (Rijndael's Advanced Encryption Standard).
Data Encryption Standard
The Data Encryption Standard (DES) has a very controversial history. It was developed on behalf of the US government based on previous work done by IBM. It was first issued in 1976 as FIPS 46, and has a 56-bit key (the key is actually 64-bits long, but it has check bits).
DES has generally been the first chose in commerce (e.g., banking).
DES has a public design which has been subject to attack by virtually all of the world's leading cryptanalysts. The publication of the standard has had the greatest affect on the development of modern day public cryptology than any other single development.
The 56-bit key length is controversial. It was originally 128, but was reduced by the NSA. The NSA also changed the configuration of the S-boxes. Many people are suspicious of the NSA's motives, and the design criteria for the algorithm was never revealed. Some suspect that there is a trapdoor in the algorithm.
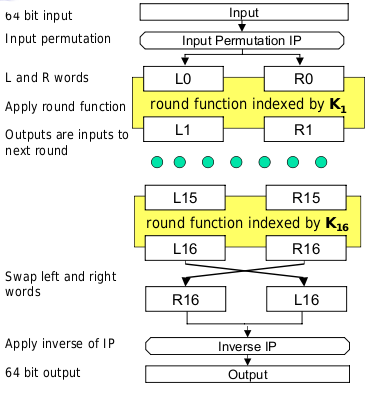
Each round is indexed by a 48-bit subkey K1 derived from the full key. 16 rounds in total are applied.
The initial permutation simply permutes the 64 bits of input according to a specific pattern. It has no security significance.
Each round takes the form given below, operating on the left and right 32-bit words. The XOR is a bitwise XOR of the 32-bit words.
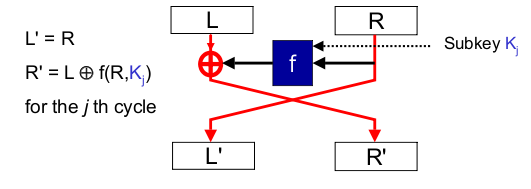
To decrypt, the same algorithm is applied with the subkeys in reverse order. The final round is followed by a swap.
Each round includes a swap, so applying a swap immediately afterwards simply undoes it. It is clear that the method simply decrypts as expected. Induction can be used to show that the property holds for an arbitrary number of rounds.
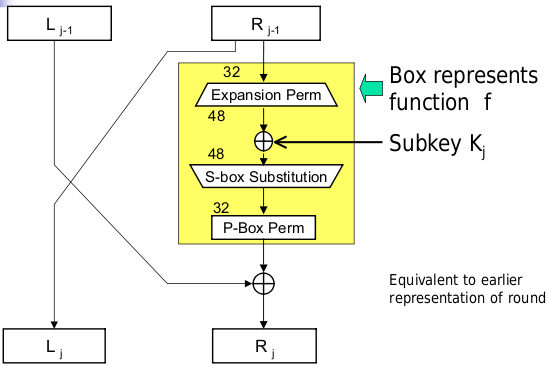
The S-boxes take 6-bit inputs and give 4-bit outputs.
All S-boxes are different and are represented using tables. For an input b, we interpret b1b6 as an integer in the range 0..3 as the row to use, and b2b3b4b5 as an integer in the range 0..15 indexing the column to use. Each entry in the table is represented by a decimal and indexed as 4-bit binary.
For the expansion and P-permutation stages, each outer bit in a block of four influences the row used to do substitution in the nearest neighbouring block of four. P-permutation is straightforward permutation.
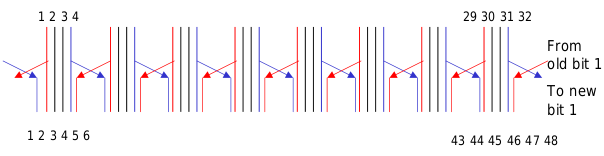
The 56-bit key is split into two 28-bit halves, and each half is subject to a cyclic shift of 1 or 2 bits in each round. After these shifts, a sub-key is extracted from the resulting halves. This is repeated for each round.
The theoretically promising cryptanalytical method of differential cryptanalysis emerged in the laste 80s, but DES was surprisingly resilient to this attack vector. Coppersmith (1994) revealed some of the design criteria, and the reason for DES's resistence to differential cryptanalysis - that it was specifically designed to be so.
This means that IBM and the NSA knew about this method of attack over 16 years before it was discovered and published by leading cryptograhpic academics.
A later technique known as linear cryptanalysis exists which DES is vulnerable to, which reduces the number of operations for a brute-force crack from 255 to 243.
Diffie & Hellman proposed a key search machine that would be able to break DES at a cost of $20M (1977), and a detailed hardware design for a key search machine was published by Wiener in 1993. The EFF in 1998 successfully cracked DES in 3 days using purpose built hardware that took less than 1 year to build at a cost of less than $250,000.
FPGAs now exist that can crack DES in 2 hours.
Advanced Encryption Standard
An interational competition was held to find a replacement for DES, which resulted in Rijndael's Advanced Encryption Standard being chosen. The competition was very public, as was the evaluation of it.
AES uses quite simple operations and appears to give good security as well as being very efficient. Many are now attacking the standard.
There are numerous standard modes of using block ciphers: electronic code book; cipher block chaining; cipher feedback moe and output feedback mode. There are some others that have been tried occasionally (e.g., propagating cipher block chaining), but we will only look at mainstream ones.
Electrionic Code Book
Electronic code book is the most primitive means of using block algorithms for message or data encryption. Successive blocks of plaintext are encrypted directly using the block cipher (the plaintext block is the input and the encrypted result is the ciphertext sent).
This leads to a problem where message blocks that contain the same values are always mapped to the same ciphertext values. Code books can be built up, where once we know that a particular block contains a certain enciphered form, we can recognise it if it occurs again. This kind of attack also occurred using classical ciphers.
More problematic is that the codebook can be used to forge messages pretending to belong to one of the legitimate communicants, as elements of messages can be replaced very easily.
This kind of encryption may be more suited to randomly accessed data (e.g., databases). ECB use is rare, and other modes are more common.
Cipher Block Chaining
There is clearly a need to mask the occurrence of identical plaintext blocks in messages. It is possibly to do this by allowing the data sent so far to affect the subsequent ciphertext blocks.
Cipher Block Chaining (CBC) is a widely used means of doing this. It XORs the plaintext block with the previously produced ciphertext block and then encrypts the result.
To recover the plaintext in such a system, you must first decrypt the appropriate ciphertext block, and then XOR it with the preceeding ciphertext block to get the plaintext.
Initial blocks are crucially important. If the same initial block is used for different messages, then it will be clear when messages have the same initial sequences. The usual solution to this is to vary the initial block in some way. There is a general notion that initial blocks should not be repeated between messages. This cna be achieved by randomess (this is generally the best), but some texts advocate simply incrementing.
The matter of initial blocks is subtle, and many texts can be downright dangerous in their advice.
Cipher Feedback Mode
If we want to transmit encrypted data a character at a time (e.g., from a terminal to a host), cipher feedback mode is often useful as it can enxrypt plaintext of a size less than the block size.
Typically 8-bit sub-blocks are used, but even 1-bit sub-blocks are possible.

We also need to consider the error propagation characteristics of the various modes of use, and the effect of a single transmission error (a bit flip) in the ciphertext.
Triple-DES is where the plaintext is first encrypted with K1, then decrypted with K2 and then re-encrypted with K1.
If K1 = K2 this is a very inefficient form of normal DES (and so can be compatible with standard DES).
Linear Cryptanalysis
Linear cryptanalysis was invented by Matsui in 1991, and is a powerful attack against many block ciphers.
It works by approximating block ciphers by means of linear expressions, which are true (or false) with some bias. This bias can be utilised to discover the key bits.
For an S-box which has 4-bit inputs (X) and 4-bit outputs (Y), two linear equations on the inputs and outputs are defined (e.g., X2 ⊕ X3 and Y1 ⊕ Y3 ⊕ Y4).
These expressions involve either inputs, or outputs, but not both. Agreement is calculated between some input expression and some output expressions, and if this differs from equal numbers of agreement and disagreement, than given a specific output expression, we have strong information on the likely value of the input expression.
Slide 8 has
an example.
This shows simply how structrual relationships between input and output that hold with some bias can be used to leak key information. Reality is a bit more sophisticated than this.
Generally ciphers are multiple round, and expressions between plaintext and intermediate ciphertext hold with some bias. To crack such a scheme, the final round is peeled off by trying all relevant subkeys and finding the one with the greatest approximation bias when evaluated. This can also be done in reverse (finding an expression that holds with a bias over rounds 2 to n which can be tested by using appropriate parts of the first key, and encrypting to obtain intermediate ciphertext).
Differential Cryptanalysis
Differential cryptanalysis is a powerful chosen plaintext attack against many block ciphers that was first published by Eli Biham and Adi Shamir.
In this attack, we work with differences. If two input X′ and X″ differ by bitwise XOR ΔX = X′ ⊕ X″, then their corresponding outputs will differ similarly by some amount: ΔY = Y′ ⊕ Y″ (where Y′ = Sbox[X′] and Y″ = Sbox[X″]).
Some characteristic pairs (ΔX, ΔY) are more common than others, and this can be used to build up a biased expression in terms of input and output differences in the same way as linear cryptanalysis.
For a given input difference, certain output differences seem to occur more often than others. In an ideal cipher, all output differences would be equally likely given an input difference, but this is actually impossible.
In this analysis we seem to join likely input-output differences over consecutive rounds. Output differences from one round feed in as the input differences to the next, in a similar fashion to that done in linear cryptanalysis. However, working with differences gives us an unexpected bonus, as the key bits cancel out.
Lecture 7 contains examples.
In a substitution-permutation network, the mth output of Si, j goes to the jth input of Si+1, m. The 16-bit subkeys are assumed independent, but in practice subkeys are often derived from a master key (as in DES). The key mixing is simply a bitwise XOR.
We can not access the intermediate ciphertext, but if we could obtain it we could use it to show that the bias was present. However, if we use correct key bits, then the two relevant ciphertext sub blocks will decrypt to the correct intermedia cipher text, and the relationship when checked will hold with a bias.
If we use the wrong key bits, then after decryption we should have the same expectation that the relationship will hold.
We can now try each target subkey in turn, and decrypt the ciphertext sub-blocks to see if whether or not the required difference holds. The number of times this is true for the target sub-key is counted, and the one with the greatest count is likely the correct target subkey.
If 10,000 plaintexts are encountered satisfying the required ΔP, then probability = count / 10000, and the largest deviation from 0 indicates the actual subkey.
However, as we mentioned above, the effect of the key disappears in differential cryptanalysis, yet it matters in the final round.
Generally, out technique has been to show that there is a structure (a relationship that holds with a bias) over n-1 rounds of the cipher, and if we can guess an idenitified subset of the final round key bits, then the structure can be checked and seen to hold with a bias. If we guess incorrectly for the subset, we do not get such a strong bias for the relationship. We can therefore tell when we have the identified subset correct, as part of the key is shouting at you - a form of divide and conquer.
We can generalise this further as there are many forms of structure, such as differences of differences, approximating sets of differentials using linear expressions, exploiting knowledge that certain differentials are impossible, having multiple approximations, or defining difference differently (bitwise XOR is simple).
We can often exploit any form of structure.
The S-boxes clearly pay an important role in the provision of security, as they provide confusion. We have seen that existence of a linear approximation leads to linear cryptanalysis, and of a differential one to differential cryptanalysis, and with this known, can S-boxes be strengthened to resist attack?
We want to avoid linear combinations of subsets of the inputs agreeing with linear combinations of subsets of the outputs. That is, we don't want expressions of the following form to hold with a bias (ωi and βj are 0 or 1): ω1x1 ⊕ … ⊕ ωnxn = β1S1(x) ⊕ … ⊕ βmSm(x).
However, the right hand side really is just a function of the inputs ƒβ(x), and so we do not want the function ƒβ(x) to agree with a linear combination of a subset of the inputs.
We can measure agreements of this form using the Walsh Hadamard values. We want the function ƒβ to have high non-linearity (a low maximum magnitude of Walsh Hadamards), but as we can choose any input subset and any output subset, we take the worst non-linearity of any derived function ƒβ(x) (i.e., over all possible β) as a measure of the strength of the S-box.
We also need to protect against the differential structure being exploited. For a simple Boolean function with one output we could measure the degree to which inputs satisfying a difference give rise to correlated outputs. We can do this using the autocorrelation function. For any input difference s the autocorrelation function r(s) is given by: r^f(s) = ∑2n-1x=0 f^(x)f^(x ⊕ s).
If ∀x, ƒ(x) = f(x + s) then this has the value 2n. Similarly, if they always disagree the value is -2n. Bent functions have zero autocorrelations for all non-zero s.
We take the highest magnitude value as an indication of the lack of differential input-output structure of a function: ACf = maxs | ∑2n-1x=0 f^(x)f^(x ⊕ s) | = maxs | r^f(s) |.
This basically means that we would like a derived linear function to have low autocorrelation (i.e., we want to reduce the biggest autocorrelation magnitude as much as possible), but we are free to chose any dervied linear approximation for the S-box. So, we calculate the autocorrelation for every possible derived linear function, and take that as an indicator of the strength of the S-box.
Deriving S-boxes with a very low autocorrelation is not easy. Getting S-boxes with high non-linearity and low autocorrelation is very hard.
Additionally, some linear and differential relationships are more worrying than others. Some research is being done into developing correlation immune and resilient S-boxes (where all the derived function are correlation immune). Additionaly, with small number of bits changing, we might want for all single bits changing that the autocorrelation is 0. This leads to a notion of propagation immunity of order 1 (a strict avalanche criterion), or more generally a propagation immunity of order k.
Brute Force Attacks
Supercomputing, dedicated crypto-hardware and special purpose re-programmable hardware (e.g., FPGAs) can be used to brute-force an algorithm - that is, try every key until it finds one that works.
Special purpose hardware is expensive but has a long history. Early examples include that designed to break the Enigma codes. Early work on the DES designs also considered special purpose hardware, and Diffie and Hellman address brute force DES attacks in 1977. Wiener gave a very detailed DES cracking design in 1993, and the EFF developed an engine that cracked the RSA Labs' DES challenge in 56 hours.
Crypto is often simple and may not take a great deal of computation. Reprogrammable hardware such as FPGAs allow software to be written and compiled down onto the reconfigurable gate arrays for computation.
Massive parallelism allows multiple programs to be compiled to one chip and run simultaneously. The different rounds of a multiple round encryption can be run simultaneously in a pipeline. An FPGA attack on DES was announced by Richard Clayton in November 2001.
The SETI@Home initiative showed that signal processing can be done all over the world as a background task. This idea has been taken up by various groups intent on finding keys or factorising primes.
A theoretical attack is called the 'Chinese radio attack'. If everyone in China had a radio with a processor capable of checking 1,000,000 keys per second, then cracking DES would take on average 30 seconds or so. At the moment this is theoretical, but with the rise of ubiquitous computing, the mechanisms may be in place to carry out similar attacks. People are happy to do signal processing on their PCs, so there should be no objection to spare-time computation on their phones or TVs.
Additionally, with every increasing supercomputer speeds brute forcing is becoming ever easier and faster.
Quantum computing allows us to dispense with the idea of distribution and allows us to carry out all computations in parallel.
In quantum computing you can place registers in a superposition of all possible states. The rules of quantum mechanics allow all states to be calculated at once. Technically, we carry out 'unitary transformations' on the state. However, there's a catch as you're only allowed to see one result. Suppose you 'look at' the final register and see either a 0 or a 1. The choice between these is random. If we see a 1 (or a 0), then the whole superposition collapses to a superposition consistent with that observation.
We then read off each register deterministically.
Unitary transformations can be used to bump up the probabilities of us seeing the result we actually want (i.e., don't leave it to luck), and this is how quantum algorithms work. The results can be surprising.
Grover's algorithm allows a state space of size 2n to be searched for satisfying a particular predicate in Ο(2n/2) iterations of a loop body. This gives us a massive increase in power.
Shor's algorith, which uses a quantum discrete fourier transform to extract periodicity information from a function, gives us the biggest result and gives rise to a polynomial time attack on RSA.
Another non-standard approach is to use DNA computing. With DNA computing, we can perform all sorts of operations on DNA strands (splitting, merging, chopping bits out, etc) and get strings to reproduce given the right environment. If we place the string in the right environmental soup, a strand of DNA will attract base elements around it to give it a complementary second strand which can be used to breed computational engines. This can be used to give us massive potential parallelism.
Another approach is to corrupt program state in some way and then infer key information from errant behaviour. Fault injection is a vector to be protected against.
Optimisation-based Approaches
Finding good boolean functions
Using the definitions of algorithm strength (non-linearity and auto-correlation), we can use search to find the best ones satisfying these criteria.
The definitions of these (given in the relevant sections above) can easily be evaluated given a function ƒ. They can therefore be used as the expressions to be optimised (and traditionally they are).
Hill Climbing
One type of search is hill climbing (local optimisation), however if started at the the wrong point we can get stuck at a local optimum. Simulated annearling is an algorithm that allows non-improving moves so that it is possible to go down in order to rise again to reach a global optimum. However, in practice the neighbourhood may be very large and the trial neighbour is chosen randomly, so it is possible to accept a worsening move when an improving one may exist.
Simulated Annealing
In simualted annealing, improving moves are always accepted, and non-improving moves may be accepted probabilistically and in a manner depending on the temperature parameter T. Loosely, the worse the move is, the less likely it is to be accepted, and a worsening move is less likely to be accepted the cooler the temperature.
The temperature T starts high and is gradually cooled as the search progresses. Initially, virtually anything is accepted, and at the end only improving moves are allowed (the search effectively reduces to hill climbing).
More formally, we can represent this as pseudo-code:
current x = x0
temp = T0
until Frozen do:
do 400 times: (at each temperature, consider 400 moves
y = generateNeighbour(x)
Δ = ƒ(x) - ƒ(y)
if (Δ > 0):
current x = y
accept (always accept improving moves)
else if (exp-Δ/Temp > U(0,1))
current x = y
accept (accept worsening moves probabilistically
else reject (it gets harder to do the worse the move)
temp = temp × 0.95
return the best so far
However, there are more advanced versions of the cost function we can consider than the simple non-linearity/autocorrelation ones above.
Parseval's theorem states ∑2n - 1ω = 0 F^(ω)2 = 22n, so loosely we can push down on F(ω)2 for some particular ω and it appears elsewhere. This suggests that arranging for uniform values of F(ω)2 will lead to good non-linearity - bent functions achieve this but we shall be concerned with balanced functions. This is the motivation for a new cost function:
cost(f) = ∑2n-1ω=0 | | F^ƒ(ω) | - X | R.
This considers the cost not for one particular input but for all inputs, to ensure that the function is optimised for all cases, not specific ones.
Moves in our search should also preserve balance. Balance is the number of 0s and 1s output. In order to preserve balance, we start with a balanced (but otherwise random) solution, and then our move strategy preserves it. This is done by defining the neighbourhood of a particular function as the set of functions obtained by exchanging two dissimilar values. We should also note that neighbouring functions have close non-linearity and autocorrelation, providing some degree of continuity.
Minimising the cost function family by itself doesn't actually give good results, but is good in getting in the right area. Our actual method is:
- Using simulated annealing to minimise the cost function given (for given parameter values of X and R), with the resulting function being ƒsa;
- Hill-climb with respect to non-linearity (using the non-linearity targeted techinque), or;
- Hill-climb with respect to autocorrelation (the autocorrelation targeted technique).
In 1995, Zheng and Zhang introduced two global avalanche criteria (autocorrelation and sum-of-squares), so autocorrelation bounds are receiving more attention. The sum-of-squares conjecture seemed to give poor results.
Another approach is correlation immunity, which seeks to punish a lack of correlation immunity (the first part of the formula) and low non-linearity. The cost function here is:
cost(ƒ) = ∑|ω|≤m | F^ƒ(ω) |R + A × maxω | F^ƒ(ω) |
We can do a linear transformation for correlation immunity. If we let WZƒ be the set of Walsh zeros of the function ƒ: WZƒ = { ω : F^ƒ(ω) = 0 } (that is, the inputs where the Walsh Hadamards are 0).
If Rank(WZƒ = n, then we can form the matrix Bƒ whose rows are the linearly independent vectors from the Walsh zeros. We can now let Cƒ = Bƒ-1 and let ƒ′(x) = ƒ(Cƒ x).
This resulting function ƒ′ has the same nonlinearity and algebraic degree and is also CI(1) - correlation immune. This can be applied to the basic functions generated earlier.
Designing Functions with Trapdoors
We can also use these techniques to plant, and detect, trapdoors left in cryptographic functions.
If we are planting a trapdoor, we first want to find a function with high non-linearity and low autocorrelation (that is, belongs in our set of Public Goodness functions - P), but also has our trapdoor function (functions in the subset of the design space - T), so we need our function to be in the set P ∩ T.
If we suppose we have an effective optimisation based approach to getting functions with this public property (P) as discussed above, we can let our cost function be cost = honest(ƒ). If we similarly had an effective optimisation technique to find functions with our trapdoor property T, we could let our cost function = trapdoor(ƒ).
We can combine the two to find a function we actually want to use: sneakyCost(ƒ) = (1 - λ) × honest(ƒ) + λ × trapdoor(ƒ), where λ is the malice factor (λ = 0 is trult honest and λ = 1 is wicked).
We want to be able to tell whether an unknown trapdoor has been inserted. Experiments have used a randomly generated vector as a trapdoor, and closeness to this vector represents a good trapdoor bias. We can investigate what happens when different malice factors are used if high non-linearity and low autocorrelation are our goodness measures.
Of all our publicly good solutions, there are two distinct subsets, those found with a honest cost function, and then with a high trapdoor bias found by combining trapdoor functions.
There appears to be nothing to distinguish the sets of solutions obtained, unless you know what form the trapdoor takes, however... If we represent two groups of functions as vectors and calculate the mean vectors, projecting one onto teh other and calculating the residual r. This represents the λ value.
Other ways we can use these approaches is to S-box design (i.e., multiple input-multiple output functions), however success has been less obvious, due to the enormity of the search space, even for small S-boxes.
Public Key Encryption
A new way of doing cryptography was published in 1976 by Whitfield Diffie and Martin Hellman, entitled New Directions in Cryptography.
Essentially, each user has two keys, a public key made available to the world (for user A, this is KA), and a private key kept secret by the user (KA-1).
This system makes possible many things that can not be done with conventional key encryption.
To send a message M in confidence to A, user B encrypts the message M using A's public key KA. A (and only A) can decrypt the message using the private key KA-1.
Some public key schemes allow the public and private keys to be used for both encryption and decryptiong (i.e., use the private key for encryption, and the public key for decryption). Thus, to send a message and guarantee authenticity, A encrypts with KA-1, and then B decrypts with KA. If the decrypted message makes sense, then B knows it came from A.
Rivest-Shamir-Adleman (RSA)
The best-known public key encryption algorithm was published in 1978 by Rivest, Shamir and Adleman, it is universally called RSA. It is based on the difficulty of factoring a number into its two constituent primes.
In practice, the prime factors of interest will be several hundred bits long.
First, we pick two large primes p and q, and calculate n = p × q. e is found relatively prime to (p - 1)(q - 1), i.e., no factor in common other than 1. We then find a d such that e × d = 1 mod (p - 1)(q - 1), e.g., using Euclid's algorithm.
e is the public key and d the private key. e and n are released to the public.
Encryption and decryption are actually the same operation: C = Me mod n and M = Cd mod n.
RSA set up a very successful company and became the world's most celebrated algorithm. However, it turns out the ideas were developed at GCHQ in the late 60s and early 70s by Ellis and Cox. Additionally, in 1974 Williamson developed an algorithm that would later be known as the Diffie-Helman algorithm.
Public key is often used to distribute keys or encrypt small amounts of data. A major problem is speed, the modular exponentiation eats up computational resources: "At it's fastest, RSA is about 1000x slower than DES" - Schneier.
Hash Functions
A hash function takes some message M of an arbitrary length and produces a reduced form, or digest, H(M) of a fixed length.
Hash functions have several desirable properties:
- Given M it is easy to compute H(M);
- Given a hash value h it is hard to compute M such that h = H(M) (i.e., hash functions are one-way);
- Given M, it is hard to find another message M′ such that H(M) = H(M′) (hash functions should be resistant to collisions).
In an open use of a hash function, sender A sends a message M together with hash value: (M, H(M)). The receiver then calculated H(M) from M and checks that the result agrees with the encrypted hash value. If so, then B may assume that the message has not been altered since it was sent, but he can not prove it was sent by A.
However, we can use hash functions in an authenticated way. If we assume A and B share a key K, then sender A sends a message M together with the encrypted hash value: (M, E(K, H(M))). The receiver then calculates H(M) and encrypts it with the key K, checking whether the result agrees with the encrypted hash value received. If it does, then B can assume that the message has not been altered since it was sent, and that the message was sent by A.
Encrypting just the hash value is faster than encrypting the whole message.
This of course assumes that A and B trust other: A can not prove that B created a message or vice-versa (either could have just made it up themselves). But with variants of public key cryptography (e.g., RSA), we can get the sender to encrypt the hash using his or her private key - we say the hash is signed.
If our hashing algorithm was not resistant to collisions, then we could monitor the network for a message (M, E(K, H(M))) and record it, and then find a message such that H(M′) = H(M), and then forge a message (M′, E(K, H(M))).
Factorisation
Pollard's Rho Method
This is a simple algorithm. If we suppose we wish to factor n, then we shall be concerned with Zn, the positive integers modulo n. We then choose an easily evaluated map from the Zn to Zn, e.g., ƒ(x) = x2 + 1 mod n.
If we start with some value x0, we generate a sequence such that: x1 = ƒ(x0), x2 = ƒ(x1) = ƒ(ƒ(x0)), x3 = ƒ(x2) = ƒ(ƒ(ƒ(x0))) …
These various x's are compared to see if there is any xj, xk such that gcd(xj - xk, n) ≠ 1. If so, we have a divisor of n (the greatest common divisor gcd(a, b) is the largest number that divides both a and b.
Essentially, we are seeking values xj and xk such that they are in the same residue classes modulo some factor r of n.
The method is faster than simply enumerating all the primes up to √. Variations on this theme exist.
Fermat Factorisation
This method is useful when n is the product of two primes that are close to one another.
We define n = a × b, t = (a + b)/2, s = (a - b)/2 so a = t + s and b = t - s, therefore n = t2 - s2.
If a and b are close, then s is small, and so t is only slightly larger than the square root of n. We then try successive values of t, t = ⌊√⌋ + 1, , t = ⌊√⌋ + 2, t = ⌊√⌋ + 3, …, until we find a value where t2 - n = s2 is a perfect square.
Fermat can be generalised. If we discovered t and s such that t2 = s2 mod n, then we have n | (t + s)(t - s), or a × b | (t + s)(t - s) (where | means divides).
a is prime and must divide one of (t + s) or (t - s), we can use gcd to find out.
However, we must be able to find appropriate congruences. Random generation is unlikely to work.
A very important method is to generate various bi such that bi2 mod n is a product of a small number of primes, and that when multiplied together give a number whose square is congruent to a perfect square mod n.
A factor base is a set of distinct primes (that we may have p1 = -1). We say that the square of an integer b2 is a B-number if the least absolute residue mod n is a product of factors from B. The least absolute residue of a mod n is the number in the range -n/2 to n/2 to which a is a congruent mod n.
Probably the most important factor base methods to emerge in recent years have been variants of the quadratic sieve developed by Pommerance. This has been the best performer for n with no factor or order of magnitude significantly less than √. The most recent is the number field sieve.
The best general purpose algorithm typically had a complexity of Ο(e(1 + ε)√)), however number field sieve has the complexity exp(Ο((log n)1/3 (log log n)2/3)).
Knapsacks
The knapsack scheme was at the heart of the first published public key scheme, but is fraught with danger.
Variants on the knapsack problem have proven of considerable interest in public key cryptography. They are not much used these days, but are of high historial importance.
If we take a sequence of positive integers B, with a super-increasing property: B = ⟨b1, …, bN - 1, bN⟩, that is b2 > b1, b3 > b2 = b1, or generically, bN > ∑N - 1j = 1 bj.
If we suppose we have a plaintext N-bit sequence p1…pN - 1pN, we encrypt this by E(p) = ∑Nj = 1 pjbj, but the plaintext can be easily recovered.
Example in lecture 14
slide 8.
By considering each value of the knapsack in decreasing order we can consider whether or not it can possibly exist in the final solution, and therefore whether the corresponding value of the key is 1 or 0.
In order to strengthen this, we can hide the super-increasing property of a sequence by transforming it in some way or another. If we start with a super-increasing knapsack B′ = ⟨b′1, …, b′N - 1, b′N⟩ and two integers (m, p) with no factors in common. A new knapsack is now formed: B = ⟨b1, …, bN - 1, bN⟩, bi = m × b′i mod p. This new knapsack is non-super-increasing.
Encryption is done as before with the new knapsack: C = E(p) = ∑Nj=1 pjbj.
To decrypt, we assume we can find an inverse to m such that m × m-1 = 1 mod p, then we can calculate:
Cm-1 mod p = ∑Nj=1 pjbjm-1 mod p
Cm-1 mod p = ∑Nj=1 pjb′jmm-1 mod p
Cm-1 mod p = ∑Nj=1 pjb′j mod p
The final form is super-increasing.
Euclid's algorithm for greatest common divisor
d | X and d | X + Y ⇒ d | Y
r0 = q1r1 + r2, r1 = q2r2 + r3, …, rm - 2 = qm - 1rm - 1 + rm, rm - 1 = qmrm, where 0 < rm < rm - 1 < … < r2 < r1
gcd(r0, r1) = gcd(r1, r2) = … = gcd(rm - 1, rm) = rm
Euclid's algorithm can be extended such: Given integers a and b with a greatest common divisor d = gcd(a, b), we can find integers r and s such that ra + sb = d. For the case where a and b are relatively prime (have no factor in common), we can find r and s such that ra + sb = 1.
Real knapsacks may have hundreds of elements. The methods of attack aren't detailed here, but there have been many knapsack variants, and virtually all have been broken. Schneir says "There have all been analysed and broken, generally using the same techniques, and litter teh cryptographic highway".
Other Schemes
Sometimes you may want to show that you have some secret, or capability, without actually revealing what it is. For example, to buy alcohol you only need to demonstrate that you are over 18 years old, though you are commonly required to additionally demonstrate who you are - this is too strong. From this, zero-knowledge schemes have been defined.
The latest research in cryptography is focussing on using quantum effects to provide provable security. Considerable strides are being made in using quantum key distribution.
Zero-Knowledge Protocols
Zero-knowledge proofs allow provers to show that they have a secret to a verifier without verifying what that sequence is.
A classic example of this is called Quisquatier and Guillou's cave. If we suppose that there is a secret to open a door in a circular cave, then if Peggy (our prover) has the secret, they can exit the cave through both ways. If not, they can only exit it the way they came in.
Victor (our verifier) stands at the entrance the cave, and Peggy enters. Victor does not see which why Peggy enters. Victor tells Peggy to either come out the right or left passage. Peggy does so, and if necessary and she has the secret, uses the door.
There is 50% chance Peggy did not need to use the door, so Victor asks Peggy to repeat the sequence, and other time the chance that Peggy never needs to use the door exponentially decreases.
Graph Isomorphisms
See GRA.
We can use tests of graph isomorphism to apply this protocol to cryptography. Graph isomorphism is a very hard problem in general and we can use this fact to allow us to demonstate knowledge of an isomorphism without revealing the isomorphism itself.
If we start with two isomorphic graphs G and G′, then Peggy generates a random isomorphism H of G and sends it to Victor. Victor then asks Peggy to prove H is isomorphic to G, or H is isomorphic to G′.
If Peggy knows the secret mapping f she is able to respond appropriately to either of these requests. For the G case, she just sends the inverse q of the random isomorphism p. For the G′ case, she responds with r = q;f. This is repeated as in the example above.
Many schemes have been proposed based on the supposed computational intractability of various NP-complete problem types. The following example shows us that the security of such schemes may be harder to ensure than it would first seem.
Perceptron Problems
Given a matrix Am × n where aij = ±1, find a vector Sn where sj = ±1, so that in the vector Am × nSn × 1, wn ≥ 0.
This problem could be made harder to imposing an extra constraint, so Am × nSn × 1 has a particular histogram H of positive values.
The suggested method to generate an instance is to generate a random matrix A, and then a random secret S, and then calculate AS. If any (AS)i < 0, then the ith row of A is negated.
However, there is significant structure in this problem, as there is a high correlation between the majority values of the matrix columns and the secret corresponding secret bits. Each matrix row/secret dot product is the sum of n Bernouilli variables. The intial histogram has Binomial shape, and is symmetric about 0, and after negation this simply folds over to be positive.
Using Search
To solve the perceptron problem, we can use search to search the space of possible secret vectors (Y) to find one that is an actual solution to the problem at hand.
We first need to define a cost function, where vectors that nearly solve the problem have a low cost, and vectors that are far from solving the problem have a high cost. We also need to define a means of generating neighbours to the current vector, and a means to determine whether to move to that neighbour or not.
Pointcheval couched the perceptron problem as a search problem. The neighbourhood is defined by single bit flips on the current solution (Y), and the cost function punishes any negative image components.
A solution to this permuted Perceptron Problem (where a Perceptron Problem solution has a particular histogram) is also a Perceptron Problem solution. Estimates of cracking the permuted Perceptron Problem on a ratio of Perceptron Problem solutions to the permuted Perceptron Problem solutions were used to calculate the size of the matrix for which this should be the most difficult: (m, n) = (m, m + 16).
This gave rise to estimates for the number of years needed to solve the permuted Perceptron Problem using annealing as the Perceptron Problem solution means that instances with matrices of size 200 could usually be solved within a day, but no Pointcheval problem instance greater than 71 was ever solved this way, despite months of computation.
Knudsen and Meier carried out a new approach in 1999, that loosely carried out sets of runs, and noted the positions where the results obtained all agree. Those elements where there is complete agreement is fixed, and new sets of runs are carried out. If repeated runs give some values for particular bits, the assumption is that those bits are actually set correctly.
This sort of approach was used to solve instances of the Perceptron Problem up to 180 times faster than the previous mechanism.
This approach is not without its problems, as not all bits that have complete agreement are correct.
An enumeration stage is used to search for the wrong bbits, and a new cost function with w1 = 30 and w2 = 1 is used with histograph punishment: cost(y) = w1costNeg(y) + w2costHist(y).
Fault Injection
What limits the ability of annealing to find a solution? A move changes a single element of the current solution, and we want current negative image values to go positive, but changing a bit to cause negative values to go positive will often cause small positive values to go negative (as it is near in the simulated annealing).
Results can be significantly improved by punishing at a positive value, which drags elements away from the boundary during the search. Using a higher exponent in differences (e.g., |wi - k|2, where k is the boundary, e.g., 4) rather than simple deviation.
With this, we can use a similar cost function as Knudsen and Meier, but with fault injection on the negativity part (and different exponents).
cost(Y) = G∑mi = 1 (max{ K - (AY)i, 0 })R + ∑ni = 1 (| Hy(i) - Hs(i) |)R.
Each problem instance is attacked using a variety of different weightings (G), bounds (K) and values of the exponent (R). This resutls in a number of different viewpoints on each problem.
The consequence is that the warped problems typically give rise to solutions with more agreement to the original secret than the non-warped ones. However, results may vary considerably, even between runs for the same problem.
Democratic viewpoint analysis is used, as it is essentially the same as Knudsen and Meier as before, but this time substantial rather than unanimous aggreement. If we choose the amount of disagreement which is tolerated carefully, we can sometimes get over half the key this way.
Timing Channel Attacks
A lot of information is thrown away, but if we monitor the search process as it slows down we can profile annealing and gain information from the timing.
This is based on the notion of thermostatistical annealing. Analysis shows that some elements will take some values early in the search and then never subsequently change (i.e., they get stuck). These ones that get stuck early often do so for a good reason - they are the correct values.
Timing profiles of warped problems can reveal significant information; the trajectory by which a search reaches its final state may reveal more information about the sought secret than the final state of the search.
Multiple clock watches analysis is essentially the same as for timing analysis, but this time the times of all runs where each bit got stuck is added up. As we might expect, those bits that often get stuck early (i.e., have low aggregate times to getting stuck) generally do so at their correct values (they take the majority value). This seems to have a significant potential, but needs some work.
What the above has shown is that search techniques have a computational dynamics too. Profiling annealing on various warped problems (mutants of the original problem) has also been looked at, and this shows an analogy with fault injection, but here it is public mathematics that is being injected.
Attacking the Implementation
If we take the purely mathematical black box crypto function approach we' have taken so far, then the input/output relation is all that can be viewed/analysed. However, crypto functions are executed on physical devices. This execution takes time and consumes power, and the precise characteristics of these are data-dependent. This can be observed and used as the basis for an attack.
A simple example here is that of safe breaking with combination dial locks. If we make the assumption that trying a combination is atomic, then we miss the intermediate stages. In reality, a sequence of tumblers fall as the dial is turned correctly, which we can attack by using a stephoscope to listen to the intermediate states as the tumblers fall. This reduces the total state space greatly, from n1 × n2 × … × nt to n1 + n2 + … + nt.
The TENEX password attack is similar. It mistakenly assumes that passwords are atomic, but in reality the password is checked byte by byte, and aborts if an incorrect byte is found. If the password is stored across a page boundary in memory, then we can watch for page faults, which occur only if all the characters up to that point are correct. This attack requires the ability to engineer the password to be stored across a page boundary in memory.
The important thing to note here is that we are observing something that is outside of the abstract model.
Timing Attacks
Many crypto algorithms calculate R = yk mod m, where y is the plaintext and k is the secret key, however exponentiation is often very large and is broken down to be more efficient.
Examples on slide 9
of lecture 11.
In base 2, if we let the binary expression of the n-bit key k be kn - 1…k1k0, then xk = yk0k1…kn-1 = (…((yk0)2 × yk1)2 … )2 × ykn - 1.
Similarly for modulo arithmetic, in general (x × Y) mod m = ((x mod m) × (y mod m)) mod m.
With this we can develop an algorithm for modular exponentiation:
s0 := 1
for i = 0 to n-1:
Ri := (if ki = 1 then (s1 × y) mod m else si)
si + 1 := (Ri × Ri) mod m
return Rn-1
We assume the attacker knows the total time to execute the algorithm for several unknown k. We notice above that the algorithm performs key-dependent multiplications, that is, it does when ki = 1, but not when ki = 0 (from line 4 of the algorithm). So, given a range of k, the attacker can collect enough information to deduce the Hamming weight (number of 1s) of each key.
This isn't very interesting, because the Hamming weight is normally approximately n/2. It is also easily blinded, by doing dummy calculations when ki = 0, e.g.,
d := (si × y) mod m
Ri := (if ki = 1 then d else si)
We can do a better attack in the same theme. If we assume the attacker knows the total time to execute the algorithm for a givem m and several known y: {(y1, t1), …, (yn, tn)}, then the data-dependent time take to perform each multiplication comes from the code:
Ri := (if ki = 1 then (si × y) mod m else si)
si+1 := (Ri × Ri) mod m
We notice that the time for each multiplication is depdendent on si, and hence on the key bits ki…k0 used so far.
Different ys result in different calculations, which will take different times, so the measured total times for the different y have a variance: σ2 = 1/N ∑Ni = 1(ti - μ)2.
The attack then emulates the algorithm for each yi. As we have assumed the attacker knows the data-dependent multiplication times, the attacker can caculate how long each round takes, assuming a key-bit value.
The first step is to calculate the time for the i = 0 loop twice, getting getting tk = 0 by assuming that k0 = 0 and tk=1 for k0 = 1, and then subtract the calculated time from the measured ti.
We can now calculate new variances of the remaining times. On average, one of the new variances is higher, and one lower than the original: σk = 02 < σ2 < σk = 12, or, σk = 12 < σ2 < σk = 02.
The smaller variance indicates the correct choice of key bit, as the correct guess subtracts off the correct times, leaving less variation in the remaining times (one algorithm loop fewer of different timings). An incorrect guess subtracts off an arbitrary time, increasing the variation in the timings.
This can then be interated. The attack progresses bit by bit, subtracting the times for the relevant calculations and the result of the previous key bit guesses. If a mistake is made, the variances start to increase (even if subsequent key bit guesses are correct, because of the wrong value of si being used in the timing calculations), indicating the attack should backtrack.
This continues until the whole key is revealed.
This attack is computationally feasible (it progresses one bit at a time), is self-correcting as erroneous guesses become apparent, and works against many obvious blinding defences (but not all).
Power Analysis
Time is not the only resource consumed by implementations; they all require some form of power, and unsurprisingly monitoring power consumption can reveal secret key information too.
To measure the power consumption of a circuit, a small (50 Ω) resistor is placed in series with the power or ground input. The voltage difference across the resistor can be used to give current (V/R=I). A well-equiped electronics lab can sample at over 1 GHz with less and 1% error, and sampling at 20 MHz or faster can now be done quite cheaply.
Simple Power Analysis
Different instructions have different power consumption profiles.
If we consider DES, we recall that each half of the key in a round is subject to a cyclic shift of 1 or 2 bits following a schedule. After the shifts, a sub-key is extracted from the resulting halves, and this is repeated for each round. These difference in cyclic shifts are what we care about.
The executing of these different paths reveals itself in the power trace as variations between rounds. These are due to conditional jumps and computational intermediates.
We can use simple power analysis to watch the algorithm execute and the conditional branches depending on key bit values (different instructions require different power for a 0 or 1), as well as other conditional branches, multiplications, etc.
It is relatively simple to blind the implementation against simple power analysis attacks by avoiding conditional branching, generating "noise", etc.
Differential Power Analysis
Differential power analysis is used to extract correlations between different executions. The structure of DES can be used to reduce the search space. We can guess some of the key bits, and then look at the correlations that exist if the guess is correct.
In DES, the initial permutation (IP) is followed by 15 rounds with crossovers of halves (remember the 16th does not have cross-over). This IP is public knowledge, so if we have the ciphertext we know L16, R16 and R15. Additionally, if we new the key for round 16 (K16), we would be able to calculate the outputs of ƒ and deduce L15 too.
For each 6-bit sub-key Ks corresponding to an identified S-box we can calculate four bits of output after the permutation, and hence four bits of L15. We define D(Ks, C) as the predictor for one of these bits.
The method here involves monitoring the power as each of m cipher-texts, C1, C2, …, Cm is produced. Each power trace is taken over some number n time steps. For each cipher-text Ci and key guess Ks, the predictor predicts either a 0 or a 1 for the identified bit.
For each key guess Ks, the predictor D(Ci, Ks) partitions the set of ciphertexts according to whether the predicted bit value is 0 or 1.
ΔD[j] = ( ( ∑mi=1 D(Ci, Ks)Ti[j] ) / ( ∑mi=1 D(Ci, Ks) ) ) - ( ( ∑mi=1 (1 - D(Ci, Ks))Ti[j] ) / ( ∑mi=1 (1 - D(Ci, Ks)) ) )
That is, the average of power samples at time step j for ciphertexts giving a predicted value of 1 minus the average of power samples at time step j for ciphertexts giving a predicted value of 0.
If a random function is used to partition the ciphertexts, then we would expect ΔD[j] to be very small. This is what happens if we guess the 6-bit S-box subkey Ks incorrectly.
If the key Ks is correct, then the predictor accurately produces two groups which are correlated with what actually happens, as we would have expected the two groups to have different power consumption averages.
For each of the 64 subkeys, we can plot values of ΔD[j] of the 64 subkey correlations against time. The correct subkey will display a prominent peak at some time, the others will not have peaks. The peak is at the time when the correct predicted bit value is being manipulated.
Countermeasures for these kind of attacks including reducing the signal strength (so leak less information, balancing Hamming weights, etc), shielding behind nouse, and destroying the correlation with blinding (hashing values, encrypting addresses, etc). However, much of this obfuscation that reduces the signal-noise ratio can be overcome by obtaining more samples.
Cryptographic Themes, Principles and Lessons
Cryptography is not just a science, but an engineering subject. Kerckhoff's principles in 1883 were invented for ciphers at the time, and can be interpreted for the modern age:
- The system should be, if not theoretically secure, unbreakable in practice;
- Compromise of the should should not inconvenience the correspondents;
- The method for choosing the particular member of the cryptographic system should be easy to memorise and change;
- The method for choosing the particular member of the cryptographic system should be easy to memorise and change;
- Ciphertext should be transmittable by telegraph;
- The apparatus should be portable;
- Use of the system should not require a long list of rules or mental strain.
One key principle of cryptography is making the design public. DES is the most controversial algorithm in cryptographic history - the biggest problem being that the design was kept secret. The problems with this are now accepted. DES's successor, AES, was determined via open competition with various analyses and the results open for all to see.
This gives rise to "ordeal by cryptanalysis". If everyone has had a go and it survives the analysis, it says something about the cipher.
Cryptanalysis as seen above can be broken into a number of classes:
- Chosen plaintext;
- Adaptive chosen plaintext attack;
- Known plaintext;
- Known ciphertext;
- Chosen ciphertext;
- Chosen key;
- Rubber cosh cryptanalysis.
Another important principle is that it is not normally worth inventing your own algorithm. Many are invented, but precious few are used. If you don't understand this principle, you won't understand how easily your algorithm will be broken.
Another recurrent theme is guess-and-check, when we can tell how good a trial of some key or sub-key is. Additionally, repetition is a problem - starting messages with the same greeting or callsign, or using block ciphers in electronic code book mode, or with the same initialisation block in CBC.
Key strategies are also important. If the key is symmetric, then it must be kept secret. In public-private key systems, the private key must be secret, but the public key is shouted to the world (maintaining integrity). Another alternative is to send it openly, but detect interference (quantum key distribution), or to bombard them with science, broadcast trillions of bits per second with only a small (unknown to the interceptor) time window actually containing the key (this is not actually implemented).
Tradeoffs are also made all the time - one time pads are perfectly secure, but logistically difficult, but other tradeoffs relate to efficiency and speed, e.g., length of public keys - 256 bit RSA used to be common, but now 2048 is recommended. Low power algorithms are also becoming important for embedded systems.
Cryptology is as much an art as a science, and in places we simply have faith in cipher security, ever conscious it could all go wrong - do you believe in the inherent difficulty of factorisation? At best, ciphers are secure against practical attack from well-established forms of attack.