Computing by Graph Transformation

Graphs

Graphs are flexible structures for representing objects and the relations between objects. They are ubiquitous in computer science, and lend themselves nicely to a natural visualisation.

A large body of mathematical knowledge has developed around graphs known as graph theory.

Graphs consist of nodes, or vertices, typically represented using dots or circles, and edges, which are represented using lines. Directed edges typically have an arrow indiciating direction. Vertices and edges in graphs can be labelled.

Different varieties of graphs exist, such as restrictons on parallel edges, or loops, or even graphs with hyperedges (edges that connect more than 2 nodes).

We can formally define a graph as so. If we let L_V be a set of node labels, and L_E a set of edge labels and L = ‹L_V, L_E›, then a graph over L is a system G = ‹ V_G, E_G, s_G, t_G, l_G, m_G ›, where V_G and E_G are finite sets of vertices and edges, s_G, t_G : E_G → V_G are functions assigning a source and a target to each edge, and l_G : V_G → L_V and m_G : E_G → L_E are functions assigning a label to each node and edge.

If V_G = ∅, then G is called the empty graph, and can be denoted by ∅.

Concrete graphs are represented in tabular form and include identifiers (note, different from labels!) for the nodes and edges. Abstract graphs are represented diagramatically and do not include the identifiers, just the structure (including labels).

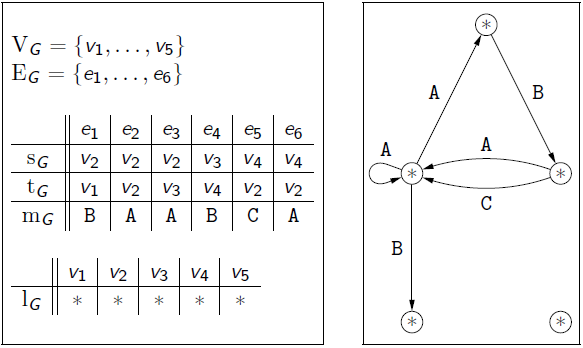
Isomorphic graphs are graphs with the same structure (abstract graph), but not necessarily the same concrete graph (i.e., the identifiers can be different).

Graph Morphisms

Given graphs G and H over L, a graph morphism g : G → H is a pair of mappings g = &lasquo; g_V : V_G → V_H, g_E : E_G → E_H &rasquo;, such that for all e ∈ E_G and v ∈ V_G:

g_V(s_G(e)) = s_H(g_E(e)) - that is, all sources are preserved;
g_V(t_G(e)) = t_H(g_E(e)) - that is, all targets are preserved;
l_G(v) = l_H(g_V(v)) - that is, node labels are preserved;
m_G(e) = m_H(g_E(e)) - that is, edge labels are preserved.

For examples, see slide 16.

We say a graph morphism g : G → H is injective, surjective or bijective if g_V and g_E are injective, subjective or bijective.

A bijective graph morphism g : G → H is an isomorphism. In this case, G and H are isomorphic, which is denoted by G =~ H (note, the ~ should be on top of the =, but I can't typeset that in HTML).

An abstract graph [G] is the isomorphism class of a graph G: [G] = { G′ | G =~ G′ }.

Given graph morphisms f : F → G, and g : G → H, the composition of g o f: G → H is defined by g o f = &lasquo; g_V o f_V, g_E o f_E &rasquo;.

For all graph morphisms f : F → G and g : G → H, g o f is a graph morphism from F to H.

Subgraphs and Inclusions

Graph G is a subgraph of graph H, denoted by G ⊆ H, if V_G ⊆ V_H, E_G ⊆ E_H, and &forall e ∈ E_G, v ∈ V_G:

s_G(e) = s_H(e);
t_G(e) = t_H(e);
l_G(v) = l_H(v);
m_G(e) = m_H(e).

A graph morphism inc : G → H is an inclusion if, ∀ v ∈ V_G, e ∈ E_G then inc_V(v) = v and inc_E(e) = e.

For all graphs G and H, G is a subgraph of H iff there is an inclusion inc : G → H.

If we consider a graph G, and subsets V ⊆ V_G and E ⊆ E_G, then there is a subgraph S of G with V_S = V and E_S = E iff ∀ e &isin E then s_G(e) ∈ V and t_G(e) ∈ V. If this property is satsified, then S is the subgraph induced by V and E.

Given a graph morphism f : G → H and a subgraph S of G, f_V(V_S) and f_E(E_S) induce a subgraph of G. The subgraph induced by f_V(V_S) and f_E(E_S) is the image of S under f and is denoted by f(S).

Transforming Graphs

The idea of graph transformation is to manipulate graphs by rules L ⇒ R, where L and R are graphs. Applying this rule L ⇒ R to a graph G replaces an occrrence of L in G with R:

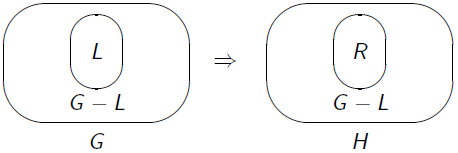
We come across problems with this though - how do we define an occurrence of L, is it a subgraph, a subgraph isomorphic to L, etc. Additionally, what happens to edges in G - L that touch nodes in L, and how is R connected to G - L?

A rule r = &lasquo; L ← K → R &rasquo; over M consists of graphs L, K and R over M, and inclusions K → L and K → R. L is the left-hand side, R is the right-hand side, and K is the interface of r.

Using these definitions, we can form the intutition that L - K is deleted, K is preserved, and R - K is added.

To apply a rule r = &lasquo; L ← K → R &rasquo; to a graph G:

Find an injective graph morphism g : L → G;
Check that no edge in G - g(L) is incident to a node in g(L - K);
Delete g(L - K) to obtain an intermediate graph D;
Add R - K to D.

Interfaces don't need to contain any edges, and should just contain nodes. In morphisms, you can just remove and put any edges back in again in L and R, instead of preserving constantly.

Additionally, rules are symmetric - left and right can be swapped. Using the double pushout method as we do, this means we can reverse steps, and dangling edges are forbidden (as upon reverse, we would not know where to connect them back to).

In the single pushout technique, dangling edges are allowed (they are discarded), but in this case, an inverse is not always obtainable as dangling edges may be lost.

Danging Condition

To deal with the problem of dangling edges (those that are left when L is deleted), we simply deny transformations on graphs where this is the case (as the resulting graph is not a graph).

So, given a rule r = &lasquo; L ← K → R &rasquo;, an injective graph morphism g : L → G satisfies the dangling condition if no edge in E_G - g_E(E_L) is incident to a node in g_V(V_L - V_K).

In other words, edges outside the occurrences of the left-hand side of the rule must not touch nodes that will be deleted.

If we let &lasquo; L ← K → R &rasquo; be arule, and g : L → G an injective graph morphism satisfying the dangling condition, then V_D = V_G - g_V(V_L - V_K) and E_D = E_G - g_E(E_L - E_K) induce a subgraph D of G and there is an injective graph morphism of d : K → D such that for all v ∈ V_K and e ∈ E_K, d_V(v) = g_V(v) and d_E(e) = g_E(e). We say that this graph morphism d : K → D is the restriction of g to K and D.

We can represent the disjoint union of two sets A and B as: A + B = (A × {1}) ∪ (B × {2}). For readability, we will usually treat A + B as A ∪ B, assuming that A and B are disjoint.

Note that there are injective functions i_A : A → A + B and i_B : B → A + B such that i_A(A) ∪ i_B(B) = A + B and i_A(A) ∩ i_B(B) = ∅.

Gluing

If we let &lasquo; L ← K → R &rasquo; be a rule and d : K → D be an injective graph morphism, then the following defines a graph H, the gluing of D and R according to d:

V_H = V_D + (V_R - V_K);
E_H = E_D + (E_R - E_K);
s_H(e) = { s_D(e) if e ∈ E_D, d_V(s_R(e)) if e ∈ E_R - E_K and s_R(e) ∈ V_K, s_R(e) otherwise;
t_H is analogous to s_H;
l_H(v) = { l_D(v) if v ∈ V_D, l_R(v) otherwise;
m_H is analogous to l_H.

We can see in our definition for source and targets we deal with 3 cases: e ∈ E_D defines nothing changing, the second case defines the target in the new bit with the source in the interface, and the third case handles where the edge is completely in the new bit less the interface.

We can also let &lasquo; L ← K → R &rasquo; be a rule, d : K → D be an injective graph morphism, and H be the gluing for D and R according to d. Now, D is a subgraph of H, and there is an injective graph morphism h : R → H such that for all x in R, h(x) = { x if x ∈ R - K, d(x) otherwise.

Direct Derivation

If we let G and M be graphs, r = lasquo; L ← K → R &rasquo; be a rule, and g : L → G be an injective graph morphism satisfying the dangling condition, then G directly derives M by r and g if M is isomorphic to the graph H constructed as follows:

D is the subgraph G - g(L - K) of G and d : K → D is the restriction of g to K and D;
H is the gluing of D and R according to d.

In this case, we write G ⇒_r,gM, or just G ⇒_r M, or G ⇒ M, and then call g the match of r in G. We also write G ⇒_R M is r belongs to a set R of rules.

Given the graphs G and H, and a set R of rules, we say that G derives H by R if G =~ H, or there is a sequence of direct derivations: G = G₀ ⇒_r₁ G₁ ⇒_r₂ ... ⇒_{r_n} G_n = H with r₁, ..., r_n ∈ R. In this case, we can just write G ⇒* H.

Graph Grammars

A graph transformation system &lasquo; L, R &rasquo; consists of a pair L = &lasquo; L_V, L_E &rasquo; of sets of node and edge labels, and a set R of rules over L.

A graph grammar is a system G = &lasquo; L, N, R, S &rasquo; such that &lasquo; L, R &rasquo; is a graph transformaion system, N = &lasquo; N_V, N_E &rasquo; and is a pair of sets of nonterminal labels with N_V ⊆ L_V and N_E ⊆ L_E, and S is a graph over L, the start graph.

The graph language generated by G consists of all graphs derivable from S by R that do not contain nonterminal labels.

For examples, see slide 41 onwwards.

Slide 48.